canvas 2d 游戏与碰撞检测

在实现 canvas 游戏和动画时往往需要解决物体相互碰撞的情况。对于物体碰撞相关的问题，一般采用碰撞检测来解决。

本文主要介绍我用 canvas 做的游戏和该游戏用到的碰撞方法，顺便简单介绍 canvas 2d 中一些通用的碰撞检测方法。

成品展示

首先贴一下游戏成品，懒得点的也可以看视频展示

游戏展示

视频展示

下面展开说其中需要处理的碰撞检测

游戏说明

游戏的目标就是控制光线，持续照亮房子一定时间即可：

但是这中间会有各种阻碍，导致房子不能直接射到房子

这个时候就需要灵活使用镜子反射光线照到房子

碰撞检测

碰撞分析

根据上面的描述，可以知道会有以下几种碰撞情况

先是当没有阻碍时，光线会跟屏幕边缘碰撞

有阻碍时，光线会在物体表面停留下来。

对页面中的图形进行抽象，可以得到我们需要处理的模型其实就是这个样子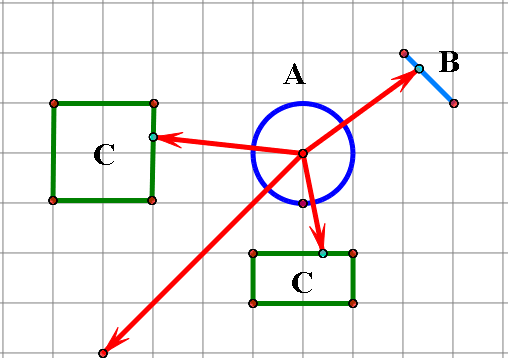

将所有碰撞检测都归为了线段和线段的相交检测，也就是图中红色线段和其他线段进行相关判断即可。

这里实现用到的原理是：一个线段会把空间分为两部分，以这个线段为分界线，判断另一个线段两个端点是否分别在这个线段分割的两个空间中。如果两个线段的两个端点都分别在另一个线段分割的两个空间中，那么就认为这两条线段是相交的。

判定两条线段是否相交，这里用到的是向量的叉乘。原理下面分析。

算法描述：设有两条线段 ab 和 cd 如图 4。当向量 ad 与向量 ac 分别位于向量 ab 的左右两端且向量 ca 与向量 cb 分别位于向量 cd 的左右两端时，线段 ab 与线段 cd 相交。

两个向量叉乘的坐标运算为：

a × b = (x1, y1, z1) × (x2, y2, z2) = (y1z2 - z1y2, z1x2 - x1z2, x1y2 - y1x2)

因为本项目的两个向量都是在同一平面上的，所以公式可以进一步简化为：

a × b = (x1, y1, 0 × (x2, y2, 0) = (0, 0, x1y2 - y1x2)

通过向量叉乘来判断两线段是否相交的原理是：在本例中，我们需要计算的叉乘是 ad×ab 和 ac×ab，ca×cd 和 cb×cd，各为一组。向量积的 z 的值只会有三种结果，正数、负数和 0。针对每一组来说，通过右手螺旋定则可以得知，当两个向量积的 z 值之积是负数的时候，两个点就会处于所选线段所分割的空间的两端，反之为正数的话便是两点在线段的同一侧，也就是两线段不想交了。

一些特殊情况的讨论：

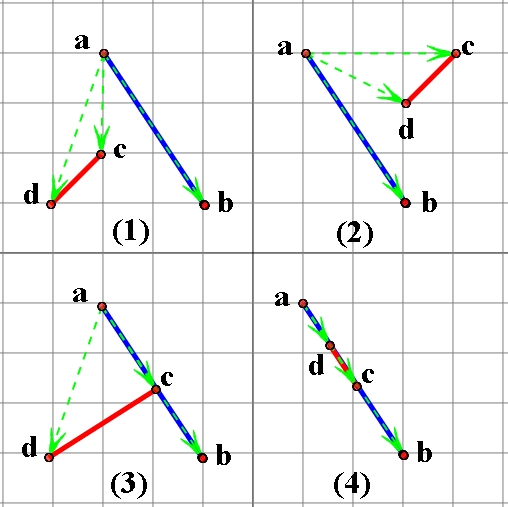
图中 1 和 2 是不相交的情况。

两个向量积的 z 值之积是 0 的时候需要分情况讨论。一种是其中一个端点在另外一条线段上（如图中 3），另外一种是两个端点都在线段上（如图中 4）。如果是第一中情况的话一组向量积中只会有一个 z 值为 0，而第二种的话则两组向量积的 z 值都会为 0。在游戏中，第一种情况也属于相交，而第二种则属于不想交。

计算交点：
在判断了两线段相交之后，就需要计算他们的交点了。因为每一个线段的端点是确定的（游戏中线段在无限延伸的情况下，会与屏幕边缘有交点，取此交点为端点），那么只需要联立两个线段的两点式方程，就可以解出交点的 x 跟 y 了。

最后是碰撞顺序的问题：

将所有碰撞都转换成线段与线段的相交检测还有一个问题，那就是顺序。因为页面中的元素位置跟大小都是不一定的，那么就需要知道，一条线段跟其余所有线段的接触的先后顺序，以确保线段不会穿过一条直线而与这条线段后面的另外一条线段相交了。

如下面图片所示：需要知道跟哪个线段先进行碰撞检测，避免出现穿过某一条线段的情况。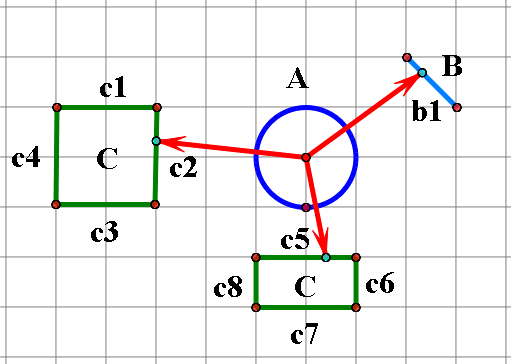

首先需要确定的是，页面中的每个元素都是由多条线段组成的。然后我们以线段的起点为圆心，只需要计算圆心到每一条线段上的一点的距离，就可以以距离升序排列所有元素，再一一和线段进行碰撞检测。显然如果直接用组成每个元素的线段来排序肯定是会有问题的，所以需要将每一条长的线段分割成很多段长度很小的线段，近似于一个点，此时再分别从这些小线段上任意取一个点加入碰撞检测的排序队列即可。

代码实现

这里仅贴出叉乘运行和交点的运算代码。

令线段一的两个端点为 p0 和 p1，令线段二的两个端点为 p2 和 p3。分别计算两组向量积的 z 值即可。
第一组向量积的 z 值，以 p0p1 向量来分割平面：

let p0p2Xp0p1 = p0p2.x * p0p1.y - p0p2.y * p0p1.x;
let p0p3Xp0p1 = p0p3.x * p0p1.y - p0p3.y * p0p1.x;

第二组向量积的 z 值，以 p2p3 向量来分割平面：

let p2p3Xp2p0 = p2p3.x * p2p0.y - p2p3.y * p2p0.x;
let p2p3Xp2p1 = p2p3.x * p2p1.y - p2p3.y * p2p1.x;

先判断 z 值的情况，若全部为 0 则表示是共线，不相交，直接结束函数。否则往下运行计算交点。

if (p0p2Xp0p1 == 0 && p0p3Xp0p1 == 0 && p2p3Xp2p0 == 0 && p2p3Xp2p1 == 0) {
  return false;
}

计算交点的时候使用的是联立两个两点式线段方程，直接得出交点的代数式，最后将交点返回即可：

let denominator = (p1.y - p0.y) * (p3.x - p2.x) - (p0.x - p1.x) * (p2.y - p3.y);
let x =
  ((p1.x - p0.x) * (p3.x - p2.x) * (p2.y - p0.y) +
    (p1.y - p0.y) * (p3.x - p2.x) * p0.x -
    (p3.y - p2.y) * (p1.x - p0.x) * p2.x) /
  denominator;
let y =
  (((p1.y - p0.y) * (p3.y - p2.y) * (p2.x - p0.x) +
    (p1.x - p0.x) * (p3.y - p2.y) * p0.y -
    (p3.x - p2.x) * (p1.y - p0.y) * p2.y) /
    denominator) *
  -1;
return { x, y };

反射

反射分析

线段的反射是游戏中重要的逻辑之一。游戏中采取的反射逻辑是光线的镜面反射，也就是入射角等于反射角。要处理这个问题，关键需要用到两个参数，一个入射光线相对基轴的角度，另一个是光线的接触面相对于基轴的角度。

在 canvas 提供的图像旋转的 api 中，是以我们普通平面坐标轴的 x 轴的负半轴为基轴，顺时针方向为正来计算角度的，所以项目中对角度的定义也是基于这一点。

如下图所示，让入射光线的角度为 α，平面角度为 β，反射光线的角度为 σ，α、β 和 σ 取值范围均为[0, 2π]。设入射角为 ∠1，反射角为 ∠2。∠1=∠2。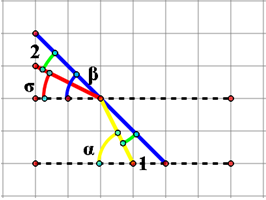

在这个分析的基础上会有下图的三种情况，反射情况的分析就不贴在这了。

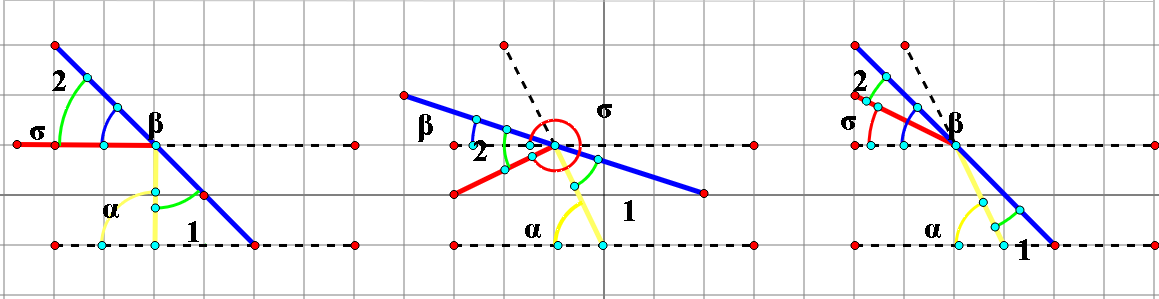
直接给出反射光线的角度为

σ = 2β - α ± 2kπ(k = 0 或 ±1)

代码实现

设入射光线的角度为 deg1，接触面的角度为 deg2，反射角度为 refAngle。依据前面的分析有：

refAngle = 2 * deg2 - deg1;

为了确保 refAngle 的取值范围为[0, 360)，还需要进一步修正 refAngle 的值，当 refAngle 大于 2π 时则需要减小 2π；当 refAngle 小于 0 时则增大 2π。修正后再返回反射角度。

if (refAngle >= 360) {
  refAngle = refAngle - 360;
} else if (refAngle < 0) {
  refAngle = refAngle + 360;
}
return refAngle;

反射的时候还需要考虑接触面的正反面问题，也就是像单面镜那样，照射到其背面是不应该会有反射的，所以在计算反射角度前还有有一个能否反射的判断，需要分别考虑光线角度小于 π 和大于 π 两种情况。

if (deg1 <= 180) {
  if (deg1 < deg2 && deg2 < deg1 + 180) {
    return true; // 可以反射
  }
  return false; // 不可以反射
} else {
  if (deg1 < deg2 || deg2 < deg1 - 180) {
    return true; // 可以反射
  }
  return false;
  不可以反射;
}

其他

还有一些物体的运动，线段的切割没有普适性，就不在此说明了。最后说一些比较通用的碰撞检测。

打飞机游戏中的碰撞检测

该部分内容均基于该教程：打飞机 - 碰撞检测。只截取主要内容，详细的分析说明请到教程中查看。

常见的碰撞检测有矩形与矩形的碰撞还有圆形和圆形的碰撞，用两张图可以简单说明这两种判定方式

矩形的碰撞：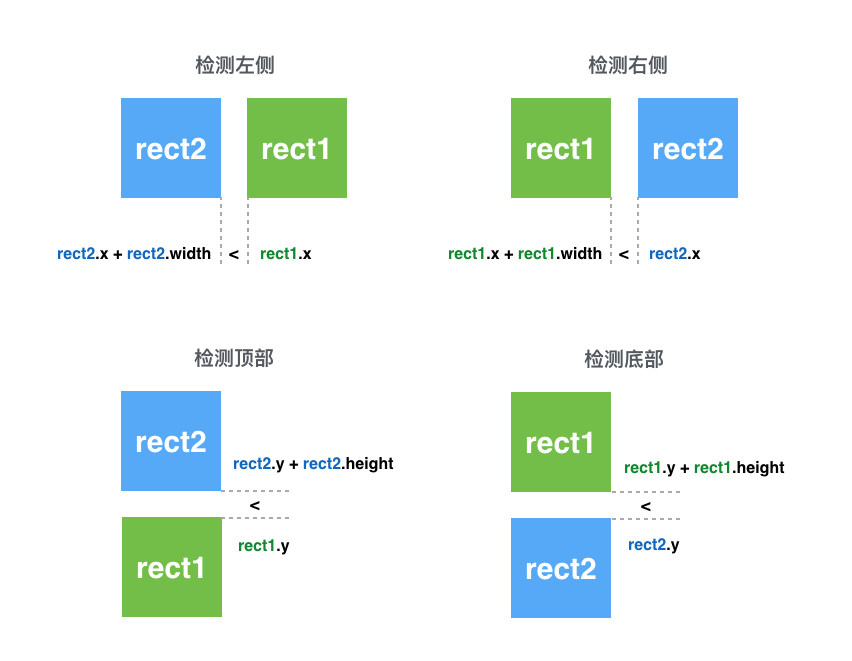

圆形的碰撞：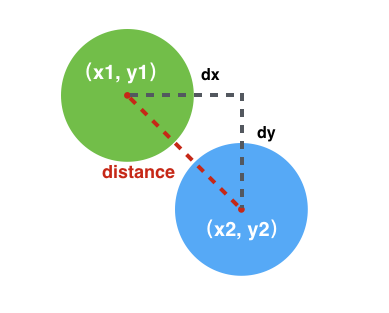

学会基础的碰撞后就可以完成一些不错的小游戏了，例如这个还未穿衣服的打飞机游戏：

给他穿上衣服就是我们常见的打飞机游戏：

常见的 2D 碰撞检测

还有一些碰撞的数学问题，感兴趣的同学可以看这篇文章：“等一下，我碰！”——常见的 2D 碰撞检测